|
You will need to read this page at least twice to understand it. That is normal.
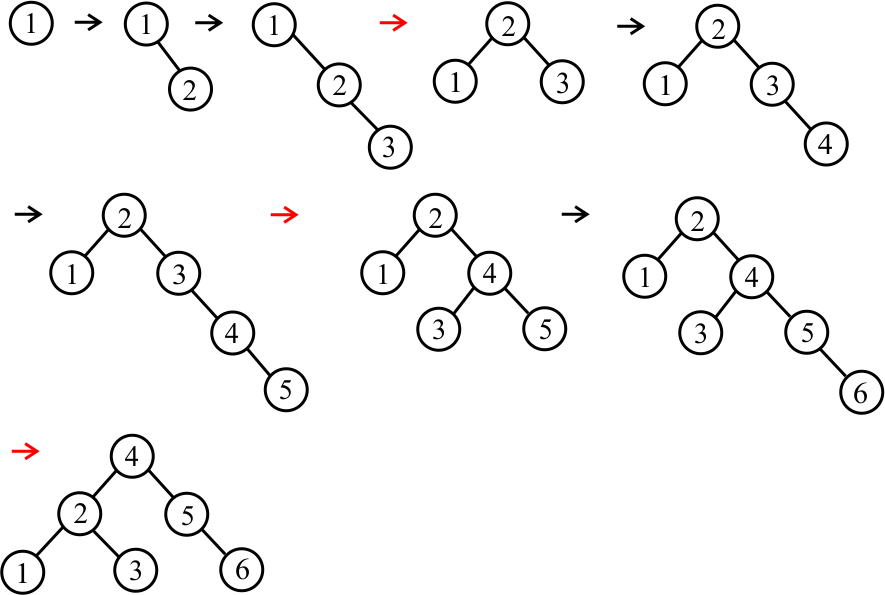
The height-balancing idea is based on performing rotations to keep the tree height balanced. As a preview, here is what happens when the numbers 1, 2, 3, 4, 5 and 6 are inserted into an initially empty tree, in that order, with rotations (indicated by red arrows) to restore balance.

After an insertion or deletion, the algorithm performs rotations where necessary. Any rotations that are necessary at node v are performed before any rotations at the parent (or any ancestor) of v. That is, rotations are done along the path upwards from the point where a change was made. If a node is already height-balanced, no rotation is called for.
The only interesting case is a node v that is not height-balanced, but whose subtrees are height-balanced (made so on the way up). Because only one insertion or deletion has been done, the height of a node can only change by 1. So the heights of the two subtrees of v must differ by exactly 2. (If the height difference is less than 2, v is already height-balanced. More than 2 would require changing a node's height by more than 1.)
Suppose that v is the root of a subtree T whose left subtree has height h+2 and whose right subtree of height h. One scheme for restoring balance is a single rotation, which works as follows. Here, x and y are integers representing the items in nodes and A, B and C are subtrees.
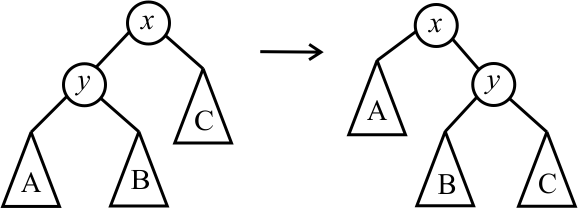
It is easy to check that a single rotation preserves the ordering requirement for a binary search tree. For example, based on the position of subtree B in the left-hand tree, all values in B must be < x and > y. That is just what is required of B in the right-hand tree.
Notice that the single rotaton has moved tree B from the left-hand side to the right-hand side. Think of it as trying to balance a scale by moving a weight from one side to the other.
There is a similar single rotation to use when the left subtree has height h and the right subtree has height h+2. It just does the rotation above backwards, from right to left.
The big question is whether performing a single rotation does any good. Is the tree surely height-balanced after doing it? We start with the following tree T.
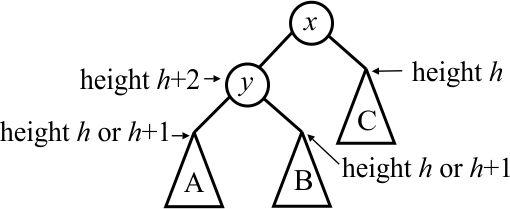
At least one of trees B and C has height h+1, since otherwise node y could not have height h+2. The other one must have height h or h+1, since the tree rooted at y is height-balanced. So we know that each of trees B and C has height h or h+1. After performing the single rotation we get the following.
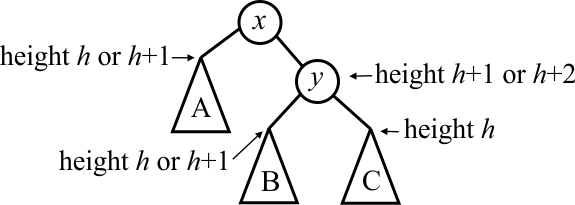
Suppose that tree B has height h. Then the tree rooted at node x has height h+1, and the entire tree is height-balanced.
But suppose that tree B has height h+1. Then the subtree rooted as x has height h+2. If tree C has height h, the tree is not height-balanced. We have moved too much from the left to the right, and have made the tree out of balance in the opposite direction. We need to do something else.
Look again at rebalancing a tree, and assume that a single rotation does not fix it. Then the heights must be as follows.
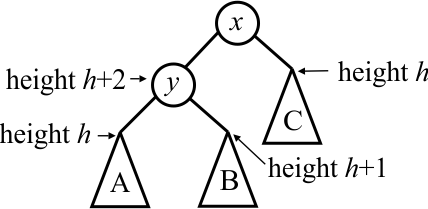
Since B has height h+1, it cannot be empty. Let's expand it one more level.
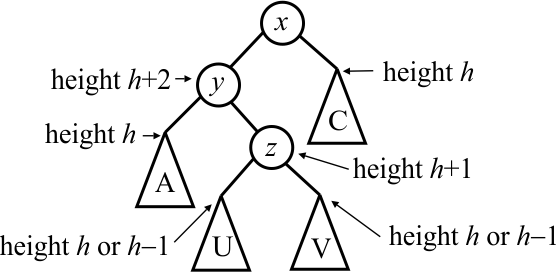
By similar reasoning as before, each of subtrees U and V has height either h or h−1. A double rotation lifts z up between x and y, yielding the following tree.
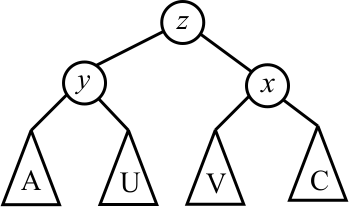
As you can see, a double rotation only moves about half of tree B from one side to the other in an effort to avoid making the tree out of balance in the opposite direction. Does it work?
The subtrees rooted at x and y each have one subtree of height h and another of height either h or h−1, so they are height-balanced. Nodes x and y each have height h+1, so the tree rooted at z is height-balanced.
There is a similar double-rotation for the case where the right subtree is 2 higher than the left subtree. See if you can see what it should be.
Suppose that you have determined that a left-to-right rotation is needed at node v, and you need to decide whether it should be a single rotation or a double rotation. Since the rotation will be from left to right, the left subtree of v is the higher of its two subtrees (by 2). Let's refer to the left child of v as y.
You can decide which kind of rotation to do by looking at the two subtrees of y. Let's refer to the left subtree of y as ℓ and the right subtree of y as r. If ℓ is higher than r, then a single rotation will work. If r is higher than ℓ, a double rotation will work.
That is an easy condition for a computer to check for, but is awkward for a human. Here is an easier way to understand it that works for both left-to-right and right-to-left rotations. To decide which kind of rotation to do at node v:
Take two steps downward in the tree, starting at v, each time toward the higher of the left and right subtrees.
If the two steps are in the same direction, either both to the left or both to the right, then it is a zig-zig. A single rotation is called for.
If the two steps are in opposite directions (one to the left and the other to the right), then it is a zig-zag, and a double rotation is called for.
For example, the following tree is out of balance at its root, and needs a rotation from right to left.

Two steps downward from the root, each time moving to the higher of the left and right subtrees, are both to the right. Since that is a zig-zig, we need to do a single rotation. The result is the following tree.
The following tree is also out of balance at its root.

This time, two steps toward the higher tree are in opposite directions. Since it is a zig-zag, a double rotation is required, yielding the following tree.

Each kind of rotation has two versions, one that moves things from right to left and one that moves things from left to right. Let's look at a left-to-right double rotation.
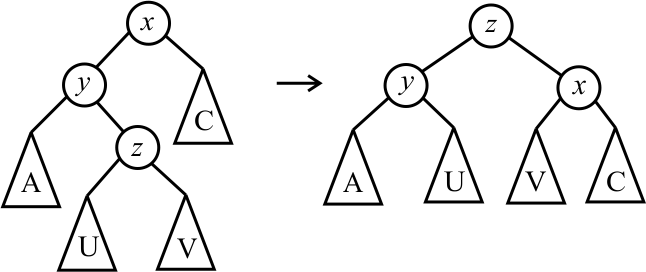
That can be accomplished in two steps, first a single rotation from right-to-left (the opposite direction) at y, then a single rotation from left to right at the root.
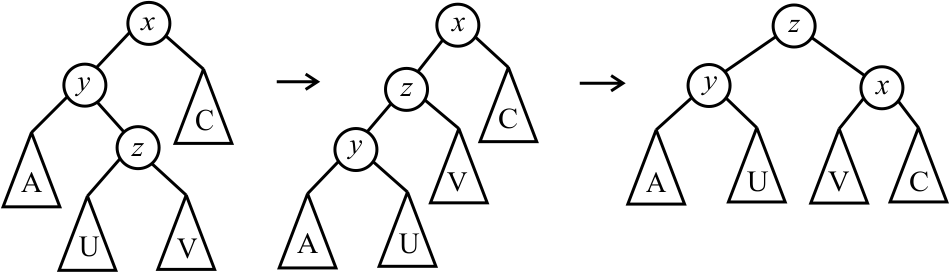
That makes the implementation of a double rotation simple: just call a single-rotation function twice.
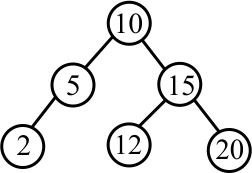
What tree do you get if you insert 4 into the following binary search tree using the algorithm that performs rotations to keep the tree height-balanced?
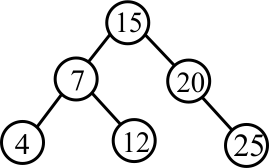
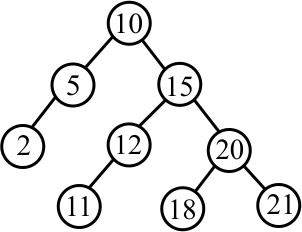
What tree do you get if you insert 25 into the following binary search tree using the algorithm that performs rotations to keep the tree height-balanced?
|