|
If list A has length m and list B has length n, then merging A and B takes m+n units of time; each time merge compares two numbers, it puts one of them into the result list and never looks at it again.
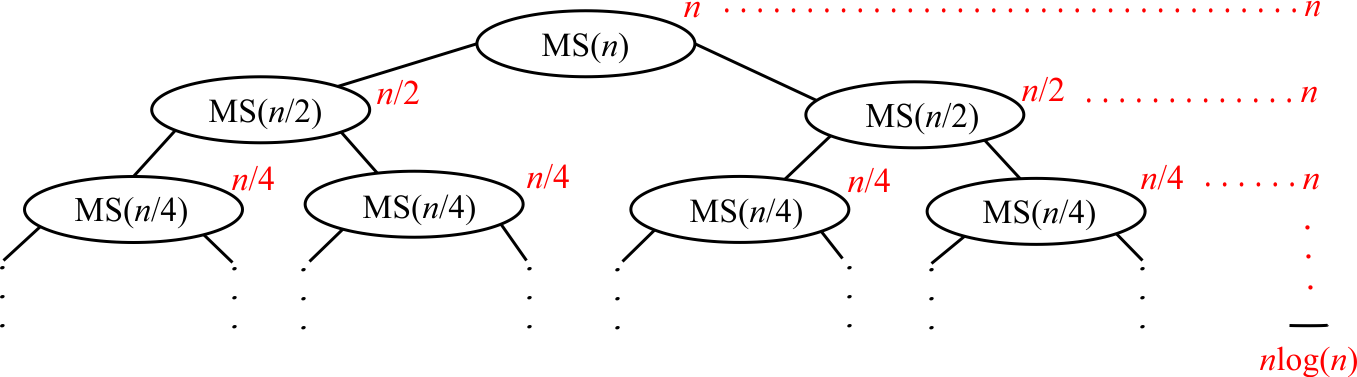
A previous lecture introduced the idea of a recursion tree, which can be used to analyze algorithms that do repeated recursive calls, as Merge Sort does. Lets apply it to find out how much Merge Sort costs.
In the following diagram, MS(n) represents a call to Merge Sort on a list of size n. Notice that it does two calls to Merge Sort on lists of size n/2. The cost of doing the merge after those recursive calls have finished is n; the cost of each node's merge is written beside it in red.

The total time spent doing merges for each level is n. So the total time, summed over all levels, is nℓ, where ℓ is the number of levels. But the sizes of the lists to sort are cut in half as you go from one level to the next. The total number of halvings before you get a list of size 1 is about log(n). So ℓ is about log(n), and the total cost of sorting a list of length n by Merge Sort is Θ(nlog(n)).
|