We have seen how to write scan algorithms using recursion, but what about search algorithms? NextPrime is easy to do.
int nextPrime(const int n)
{
if(isPrime(n+1))
{
return n+1;
}
else
{
return nextPrime(n+1);
}
}
That is, if n+1 is prime, then the smallest prime number that is greater than n must be n+1. But if n+1 is not prime, then get the smallest prime number that is greater than n+1.
Recall that we used a loop to write a definition of member(x, A, n), which returns true if at least one of the values A[0], … A[n−1] is equal to x. Let's do it using recursion. There are three cases. Each assumes that the preceding cases did not apply.
Member(x, A, n) asks whether any of the first n variables in array A holds x. If n = 0, then that cannot possibly be true, since there are no values to look at.
If A[n−1] = x, then yes, one of A[0], …, A[n−1] is equal to x. (Note that it is critical to handle the case where n = 0 first. If n = 0 then n−1 = −1, and there is no such thing as A[−1].)
If neither of the preceding cases is applicable, then n > 0 and A[n−1] ≠ x. In that case, member(x, A, n) is true if and only if member(x, A, n−1) is true. (We can ignore A[n−1] since it is not equal to x.)
Here is a definition of member based on those observations.
bool member(const int x, const int A[], const int n)
{
if(n == 0)
{
return false;
}
else if(A[n-1] == x)
{
return true;
}
else
{
return member(x, A, n-1);
}
}
Carrying on the same ideas, here is a recursive definition of allPositive. Note that allPositive(A, 0) is true, since there are not any non-positive numbers among the first 0 members of array A.
bool allPositive(const int A[], const int n)
{
if(n == 0)
{
return true;
}
else if(A[n-1] <= 0)
{
return false;
}
else
{
return allPositive(A, n-1);
}
}
There is a special kind of recursion where the cost of using recursion is much smaller than in the general case. Tail recursion is a situation where a recursive call is the last thing a function does before returning, and the function either returns the result of the recursive call or (when the return type is void) returns no result.
Look at the function definitions above. The recursive call in nextPrime is
return nextPrime(n+1);That is tail recursion. The function does nothing with the result of the recursive call except to return it. The recursive call in the definition of member,
return member(x, A, n-1);is also tail recursion, as is the recursive call
return allPositive(A, n-1);in the definition of allPositive. Of course, there are non-tail recursive calls. The recursive call in the definition of sum on the previous page,
return sum(A, n-1) + A[n-1];is not tail-recursive. After getting the result sum(A, n−1), sum adds A[n−1] to that result.
So what is the significance of tail recursion? A compiler can recognize tail recursion and replace it by a loop, making it more efficient in both time and memory.
For illustration, let's convert the recursive definition of allPositive to a loop. Here is the starting point.
bool allPositive(const int A[], const int n)
{
if(n == 0)
{
return true;
}
else if(A[n-1] <= 0)
{
return false;
}
else
{
return allPositive(A, n-1);
}
}
Because the recursive call is tail recursive, nothing in a given frame of allPositive needs to be remembered when the recursive call is done. After all, none of that information will be used. The compiler can safely convert it to changing the parameters and going back to the beginning.
bool allPositive(const int A[], const int n)
{
while(true)
{
if(n == 0)
{
return true;
}
else if(A[n-1] <= 0)
{
return false;
}
else
{
n = n - 1;
// continue the loop.
}
}
}
You would not be allowed to change the value of n, since it is a const parameter. But the compiler is not bound by that restriction; it can do whatever it wants to do, as long as the translated program works correctly according to the rules of C++.
The nice thing about tail recursion is that you do not convert it to a loop; you can let the compiler do that. The recursive definition might be easier to write.
Most compilers only convert tail recursion to a loop when asked to optimize. The g++ compiler will do that conversion if you use command-line option -O.
In terms of algorithm efficiency, recursion is an amplifier. If you do something that is a little bit good, recursion can amplify that to make it very good. But the flip side is that, if you do something a little bad, recursion amplifies it and makes it very bad.
To illustrate, suppose that you have an array A of integers of size n (where n > 0), and you want to find the largest value in the array.
If n = 1, then the largest value is just A[0].
If n > 1 then the largest value is the larger of A[n−1] and the largest of the first n−1 values in the array.
Here is a definition of largest for consideration.
// largest(A,n) yields the largest of
// A[0], A[1], ..., A[n-1].
int largest(const int A[], const int n)
{
if(n == 1)
{
return A[0];
}
else if(A[n-1] > largest(A, n-1))
{
return A[n-1];
}
else
{
return largest(A, n-1);
}
}
That will compute the correct answer, but it is
very slow. The problem is that, when
largest(A, n−1) > A[n−1],
this function computes
largest(A, n−1) twice, once in the test and once
in the return statement.
Recursion amplifies that. If the largest value in the array is in A[0], then this function takes at least 2n steps to find the largest value. If n = 200, then 2n is much larger than the number of protons in the earth! The reason is below.
It is easy to fix the problem. Just make sure not to compute largest(A, n−1) more than once.
// largest(A,n) yields the largest of
// A[0], A[1], ..., A[n-1].
int largest(int A[], int n)
{
if(n == 1)
{
return A[0];
}
else
{
return max(A[n-1], largest(A, n-1));
}
}
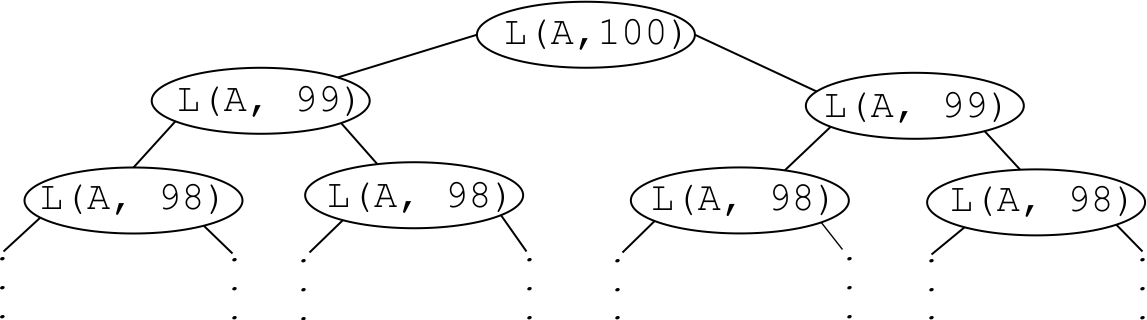
Why is the original algorithm for largest so slow? Imagine that the largest value is in A[0]. Then the last case is taken for all values of n > 1. Let's show a computation of largest(A, 100) in a tree diagram. Each node in the tree represents a call to largest. (L stands for largest.)

Each level in the tree has twice as many nodes as the level above it. There are 299 nodes in the level whose nodes say L(A, 1).
Using recursion, write a definition of ascending(A, n), which returns true if A[0], … A[n−1] are in strictly ascending order, where A is an array of integers. If n = 1, the array is in ascending order. Answer
What is the advantage of tail-recursion over general recursion? Answer
Is the following definition of g tail-recursive?
int g(int n)
{
if(n == 1)
{
return 2;
}
else
{
return g(n-1) + 3;
}
}
Answer
Write a definition of factorialTimes(n, m), which returns m*n!. Make the definition use tail recursion. Answer