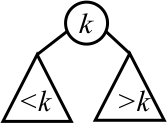
A binary search tree is a binary tree with the following property.
| If a given node v has item k, then all nodes in the left subtree of v have items that are less than k, and all nodes in the right subtree of v have items that are greater than k. |

For example, the following is a binary search tree.

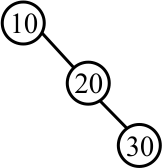
A binary search tree can have any shape, as long as it obeys the ordering requirement. The following is a binary search tree. (The left subtree of each node is an empty tree.)
Our intent is to use a binary search tree as an implementation of a set of integers, namely, the set of integers that occur in the tree. An empty tree represents an empty set.
Functions can take advantage of the ordering requirement in a way that is similar to what binary search does. A membership testing function can exploit the following facts.
An empty tree has no members.
If the root of T contains x, then tree T clearly contains x.
If the root of T contains k and x < k then, if x occurs in T at all, it must occur in T 's left subtree, by the ordering requirement for binary search trees.
Similarly, if the root of T contains k and x > k, then x occurs in T if and only if x occurs in T 's right subtree.
//==========================================
// member
//==========================================
// member(x,T) returns true if x is in binary
// search tree T.
//==========================================
bool member(const int x, const Tree T)
{
if(T == NULL)
{
return false;
}
else if(x == T->item)
{
return true;
}
else if(x < T->item)
{
return member(x, T->left);
}
else
{
return member(x, T->right);
}
}
Notice the similarity between that and binary search.